Логистическая регрессия

Это вероятность того, что \(y = 1\) при текущих входных параметрах \(x\)

\begin{equation} \hat{y} = P(y=1|x) \\ \hat{y} = \sigma{}(w^{T}x + b) \end{equation}

\begin{equation} z = w^{T}x + b \end{equation}

Ограничивает значение \(\hat{y}\) между \(0\) и \(1\).

\begin{equation} \sigma{}(z) = \frac{1}{1+e^{-z}} \end{equation}

• Если значение \(z\) сильно больше \(0\), то

  \begin{equation} \sigma{}(z) \approx{} \frac{1}{1+0} \approx{} 1 \end{equation}

• Если значение \(z\) сильно меньше \(0\), то

  \begin{equation} \sigma{}(z) \ approx{} \frac{1}{1+bignum} \approx{} 0 \end{equation}

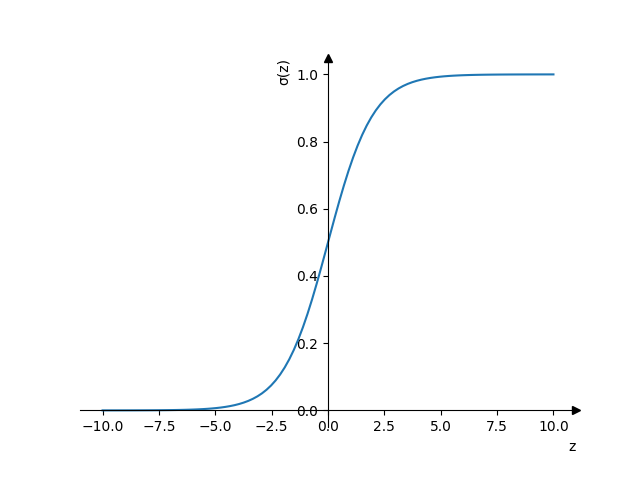
sigmoid

\(a = \frac{1}{1+e^{-z}}\)

• Значения будут от 0 до 1.
• Стоит применять только для выходного слоя
• Andrew Ng рекомендует никогда не использовать эту функцию активации кроме как для выходного слоя

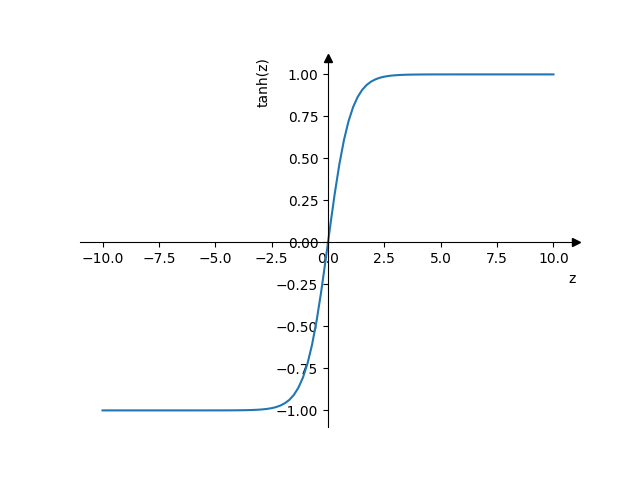
tanh

\(a = \tanh(z) = \frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}\)

• Значения от -1 до 1, что значительнее удобнее чем [0,1] у сигмоиды в плане центрирования данных вокруг нуля.
• Почти всегда лучше чем сигмоида (исключение: выходной слой)

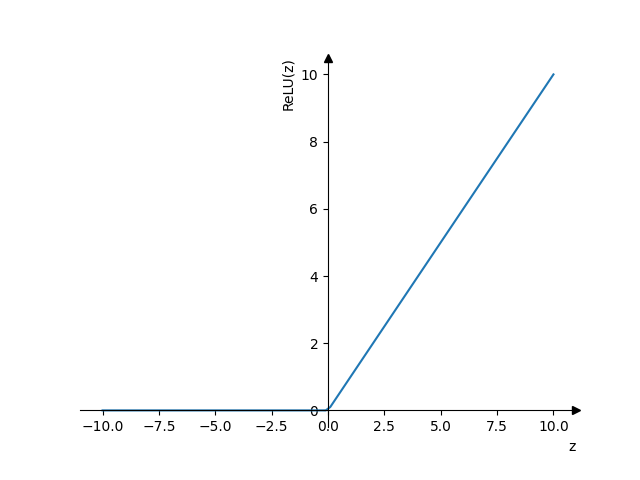
ReLU (Rectified Linear Unit)

\(a = max(x, 0)\)

• подходит для большинства случаев
• работает быстрее всего

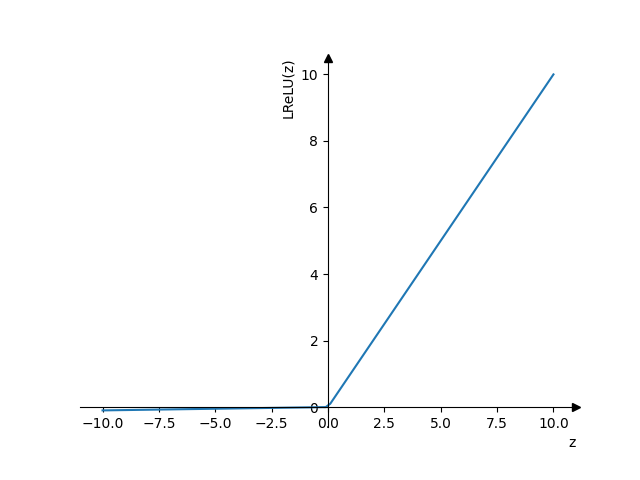
Leaky ReLU

\(a = max(0.01z, z)\)

• Работает лучше чем ReLU, но редко используется на практике
• Решает проблему ReLU с тем, что для отрицательных значений backpropagation будет занулять параметры

\(z^{[l]} = w^{T}x + b\)

\(L\)

глубина нейройной сети (количество слоёв, кроме входных параметров)

\(n^{[l]}\)

количество нейронов в слое \(l\)

\(|z^{[l]}|\)

\(z^{[l]} : (n^{[l]}, 1)\)

\(|a^{[l]}|\)

\(a^{[l]} : (n^{[l]}, 1)\)

\(|x^{[l]}|\)

\(x^{[l]} : (n^{[l-1]}, 1)\)

\(|w^{[l]}|\)

\(w^{[l]} : (n^{[l]}, n^{[l-1]})\)

\(|dw^{[l]}|\)

\(dw^{[l]} : (n^{[l]}, n^{[l-1]})\)

\(|b^{[l]}|\)

\(b^{[l]} : (n^{[l]}, 1)\)

\(|db^{[l]}|\)

\(db^{[l]} : (n^{[l]}, 1)\)

\(m\)

размер тренировчоных данных

\(|Z^{[l]}|\)

\(Z^{[l]} : (n^{[l]}, m)\)

\(|dZ^{[l]}|\)

\(dZ^{[l]} : (n^{[l]}, m)\)

\(|A^{[l]}|\)

\(A^{[l]} : (n^{[l]}, m)\)

\(|dA^{[l]}|\)

\(dA^{[l]} : (n^{[l]}, m)\)

\(|W^{[l]}|\)

\(W^{[l]} : (n^{[l]}, n^{[l-1]})\)

\(|X^{[l]}|\)

\(X^{[l]} : (n^{[l-1]}, m)\)

\(|B^{[l]}|\)

\(B^{[l]} : (n^{[l]}, 1)\)