работа с графами в Python

1. Граф
2. Depth-First Search — Поиск вглубину
3. DFS Paths — поиск пути между двумя вершинами
4. Bread-Firsth Search — Поиск вширину
5. BFS Paths

1 Граф

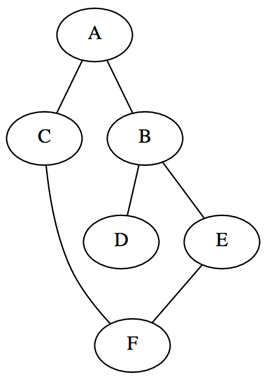
Будет использоваться ненаправленный связный граф V=6 E=6. Существует две популярные методики представления графов: матрица смежности (эффективна с плотными графами) и список связей (эффективно с разряженными графами). Будем использовать второй способ.

graph = {'A': ['B', 'C'],
         'B': ['A', 'D', 'E'],
         'C': ['A', 'F'],
         'D': ['B'],
         'E': ['B', 'F'],
         'F': ['C', 'E']}

2 Depth-First Search — Поиск вглубину

Алгоритм поиска вглубину: исследуем сначала все возможные вершины (из выбранного корня) доступные из текущей, прежде чем возвращаться назад. Данный алгоритм можно реализовать как рекурсивно, так и итеративно. Последовательность действий:

Помечаем текущую вершину как посещённую
Исследуем каждую соседнюю вершину не включённую в список уже посещённых
Вариант с DFS and BFS in Python (модифицированный, т.к. set не поддерживает упорядоченность элементов)

graph = {'A': ['B', 'C'],
         'B': ['A', 'D', 'E'],
         'C': ['A', 'F'],
         'D': ['B'],
         'E': ['B', 'F'],
         'F': ['C', 'E']}

def dfs(graph, start):
    visited, stack = [], [start]
    while stack:
        vertex = stack.pop()
        if vertex not in visited:
            visited.append(vertex)
            stack.extend(set(graph[vertex]) - set(visited))
    return visited

print(dfs(graph, 'A'))

['A', 'C', 'F', 'E', 'B', 'D']

Вариант с DFS and BFS graph traversal (Python recipe) (модифицированный, т.к. для реализации стека нам необходимо добавлять элементы в конец списка, а не в начало)

graph = {'A': ['B', 'C'],
         'B': ['A', 'D', 'E'],
         'C': ['A', 'F'],
         'D': ['B'],
         'E': ['B', 'F'],
         'F': ['C', 'E']}


def iteractive_dfs(graph, start, path=None):
    """iterative depth first search from start"""
    if path is None:
        path = []
    q = [start]
    while q:
        v = q.pop()
        if v not in path:
            path = path + [v]
            q += graph[v]
    return path

print(iteractive_dfs(graph, 'A'))

['A', 'C', 'F', 'E', 'B', 'D']

3 DFS Paths — поиск пути между двумя вершинами

graph = {'A': ['B', 'C'],
         'B': ['A', 'D', 'E'],
         'C': ['A', 'F'],
         'D': ['B'],
         'E': ['B', 'F'],
         'F': ['C', 'E']}

def dfs_paths(graph, start, goal):
    stack = [(start, [start])]  # (vertex, path)
    while stack:
        (vertex, path) = stack.pop()
        for next in set(graph[vertex]) - set(path):
            if next == goal:
                yield path + [next]
            else:
                stack.append((next, path + [next]))

print(list(dfs_paths(graph, 'A', 'F')))

[['A', 'C', 'F'], ['A', 'B', 'E', 'F']]

4 Bread-Firsth Search — Поиск вширину

Позволяет найти кратчайший путь между двумя вершинами. Довольно сложно реализовать рекурсивно, гораздо проще реализовать его с использованием очереди.

graph = {'A': ['B', 'C'],
         'B': ['A', 'D', 'E'],
         'C': ['A', 'F'],
         'D': ['B'],
         'E': ['B', 'F'],
         'F': ['C', 'E']}
from queue import deque


def bfs(graph, start):
    visited, queue = [], deque([start])
    while queue:
        vertex = queue.pop()
        if vertex not in visited:
            visited.append(vertex)
            queue.extendleft(set(graph[vertex]) - set(visited))
    return visited

print(bfs(graph, 'A'))

['A', 'B', 'C', 'D', 'E', 'F']

5 BFS Paths

from queue import deque
graph = {'A': ['B', 'C'],
         'B': ['A', 'D', 'E'],
         'C': ['A', 'F'],
         'D': ['B'],
         'E': ['B', 'F'],
         'F': ['C', 'E']}


def bfs_paths(graph, start, goal):
    queue = deque([(start, [start])])
    while queue:
        (vertex, path) = queue.pop()
        for next in set(graph[vertex]) - set(path):
            if next == goal:
                yield path + [next]
            else:
                queue.appendleft((next, path+[next]))

print(list(bfs_paths(graph, 'A', 'F')))


def shortest_path(graph, start, goal):
    try:
        return next(bfs_paths(graph, start, goal))
    except StopIteration:
        return None

print(shortest_path(graph, 'A', 'F'))
print(shortest_path(graph, 'E', 'D'))
print(shortest_path(graph, 'A', 'D'))
print(shortest_path(graph, 'F', 'D'))

[['A', 'C', 'F'], ['A', 'B', 'E', 'F']]
['A', 'C', 'F']
['E', 'B', 'D']
['A', 'B', 'D']
['F', 'E', 'B', 'D']